预测鲍鱼的年龄

数据y=1*b+a*x
1 0.455 0.365 0.095 0.514 0.2245 0.101 0.15 15
...

其中1 0.455 0.365 0.095 0.514 0.2245 0.101 0.15为参数

15为y

使用前100行数据生成参数并验证
yHat01=lwlrTest(abX[0:99],abX[0:99],abY[0:99],0.1);

使用前100行数据生成参数并使用100-200行数据验证
yHat01=lwlrTest(abX[100:199],abX[0:99],abY[0:99],0.1);


计算平方误差
((yArr-yHatArr)**2).sum()
其中yArr是原始数据,yHatArr是使用参数得到的数据


前100条做测试集
56.83512842240429  k=0.1
429.8905618701634  k=1
549.1181708823923  k=10
结论:
不在所有数据集上都使用最小的核,因为使用最小的核将造成过拟合

101-200条做测试集
41960.42296690966  k=0.1
573.5261441899764  k=1
517.5711905380314  k=10
结论:
核大小等于10时的测试误差最小

最终结论:
必须在未知数据上比较效果才能选取到最佳模型

缩减系数来“理解”数据
上面方法的缺陷
如果数据的特征比样本点还多,不能再使用前面介绍的方法。这是因为在计算 (X T X) -1 的时候会出错,特征比样本点还多（ n > m ） ，也就是说输入数据的矩阵 X 不是满秩矩阵。非满秩矩阵在求逆时会出现问题


第一种缩减方法:岭回归

回归系数的计算公式将变成：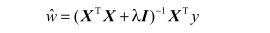


岭回归就是在矩阵 XT X 上加一个λ I 从而使得矩阵非奇异，进而能对 X T X +λ I 求逆

lasso法:


第二种缩减方法:前向逐步回归