普通最小二乘法讲解OLS线性回归

Poblog 05月24日 2018

原始数据  1 x  y  最终拟合为y=a*x+1*b
1.000000 0.067732 3.176513
...


xArr: [[1.0, 0.067732], [1.0, 0.42781], ...]

yArr: [3.176513, 3.816464, 4.550095,...]

矩阵转换
xMat：n*2
[[1.       0.067732]
 [1.       0.42781 ]
 ....]


yMat:n*1
[[3.176513]
 [3.816464]
 ...]


平方误差

普通最小二乘法讲解OLS

系数求法公式:


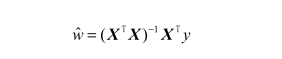
矩阵的逆可能并不存在，因此必须要在代码中对此作出判断


xMat.T是xMat的转置  2*n

矩阵行列式 xTx=xMat.T*xMat  2*n *  n*2 =2*2

xTx:
 [[200.          97.6638    ]
 [ 97.6638      64.76838373]]

求矩阵的行列式，矩阵行列式|A|=0,则矩阵不可逆
判断 np.linalg.det(xTx)==0.0

求得为:3415.4589150723973

按照公式求出系数矩阵
 ws=xTx.I*(xMat.T*yMat)

 ws=
 [[3.00774324]
 [1.69532264]]


画出散点和拟合直线

XMat:n*2
YMat:n*1

yHat=XMat*ws; 求出用拟合系数得到的y值

对照公式解释如下:
[[1.       0.067732]
 [1.       0.42781 ] 
 ....]
* [[3.00774324]
 [1.69532264]]

y=ax+b来说,

 1. 是b的系数 3.00774324是b   
 0.067732是x  1.69532264是a

求得的yHat如下,对应上面公式的一系列y值
[[3.12257084]
 [3.73301922]
 ....]


作图参数:
x:XMat[:,1].flatten().A[0]
y:YMat.T[:,0].flatten().A[0]

ax.scatter(XMat[:,1].flatten().A[0],YMat.T[:,0].flatten().A[0])

ax.plot(XMat[:,1].flatten().A[0],yHat)

画出最终图如下:



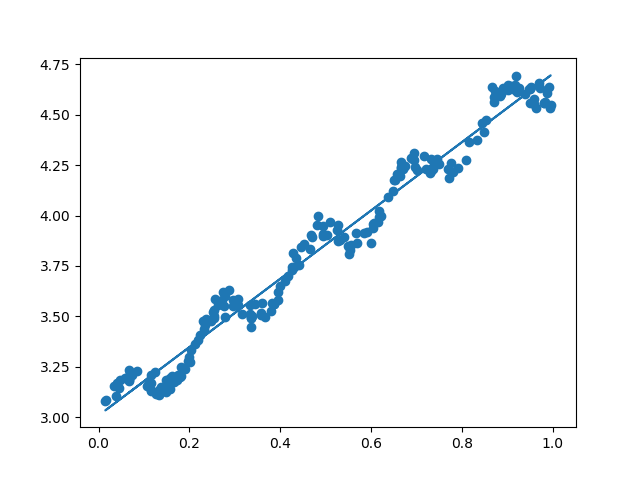
出现新的点需要预测则带入yHat=XMat*ws;求出即可


评估拟合直线的好坏(相关系数)


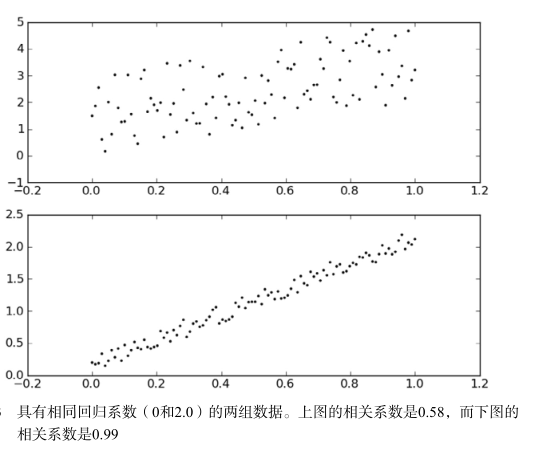
NumPy库提供了相关系数的计算方法 corrcoef(yEstimate,
yActual)
前一个是参数预测值，后一个参数是真实值，相关系数越大则拟合效果越好
上面这个例子的相关系数corrcoef计算得到

relate=np.corrcoef(yHat.T,
YMat);

[[1.         0.98647356]
 [0.98647356 1.        ]]

 即相关系数为0.98647356