Logistic回归

Poblog 05月15日 2018

Logistic回归

最优化算法

海维塞德阶跃函数在跳跃点上从0瞬间跳跃到1,这个瞬间跳跃过程有时很难处理。Sigmoid函数也有类似的性质,且数学上更易处理,如果横坐标刻度足够大,Sigmoid函数看起来很像一个阶跃函数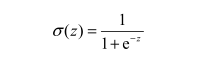


在每个特征上都乘以一个回归系数，然后把所有的结果值相加，将这个总和代入Sigmoid函数中，进而得到一个范围在0~1之间的数值。任何大于0.5的数据被分入1类，小于0.5即被归入0类。所以，Logistic回归也可以被看成是一种概率估计

最佳回归系数确定

Sigmoid函数的输入Z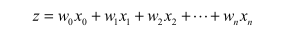



梯度上升法
思想:要找到某函数的最大值，最好的方法是沿着该函数的梯度方向探寻

f(x,y) 的梯度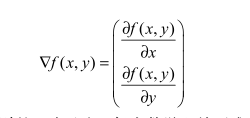


Logistic回归分类器的应用例子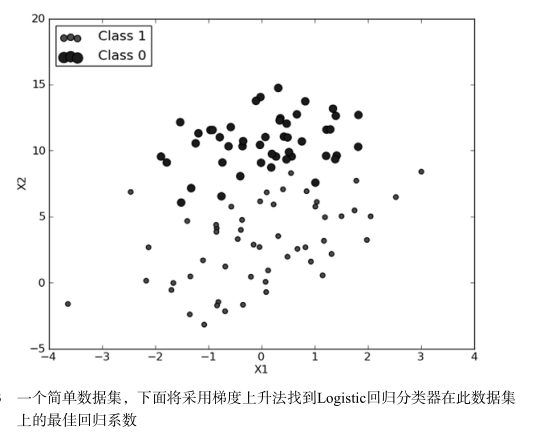


使用梯度上升找到最佳参数

依次读入文件数据到数组

lineArr:['-0.017612', '14.053064', '0']

dataMat:[[1.0, -0.017612, 14.053064]]

labelMat: [0]
...
最终数据如下:
dataMat: [[1.0, -0.017612, 14.053064], [1.0, -1.395634, 4.662541], [1.0, -0.752157, 6.53862], [1.0, -1.322371, 7.152853], [1.0, 0.423363, 11.054677], [1.0, 0.406704, 7.067335], [1.0, 0.667394, 12.741452], [1.0, -2.46015, 6.866805], [1.0, 0.569411, 9.548755], [1.0, -0.026632, 10.427743], [1.0, 0.850433, 6.920334], [1.0, 1.347183, 13.1755], [1.0, 1.176813, 3.16702], [1.0, -1.781871, 9.097953], [1.0, -0.566606, 5.749003], [1.0, 0.931635, 1.589505], [1.0, -0.024205, 6.151823], [1.0, -0.036453, 2.690988], [1.0, -0.196949, 0.444165], [1.0, 1.014459, 5.754399], [1.0, 1.985298, 3.230619], [1.0, -1.693453, -0.55754], [1.0, -0.576525, 11.778922], [1.0, -0.346811, -1.67873], [1.0, -2.124484, 2.672471], [1.0, 1.217916, 9.597015], [1.0, -0.733928, 9.098687], [1.0, -3.642001, -1.618087], [1.0, 0.315985, 3.523953], [1.0, 1.416614, 9.619232], [1.0, -0.386323, 3.989286], [1.0, 0.556921, 8.294984], [1.0, 1.224863, 11.58736], [1.0, -1.347803, -2.406051], [1.0, 1.196604, 4.951851], [1.0, 0.275221, 9.543647], [1.0, 0.470575, 9.332488], [1.0, -1.889567, 9.542662], [1.0, -1.527893, 12.150579], [1.0, -1.185247, 11.309318], [1.0, -0.445678, 3.297303], [1.0, 1.042222, 6.105155], [1.0, -0.618787, 10.320986], [1.0, 1.152083, 0.548467], [1.0, 0.828534, 2.676045], [1.0, -1.237728, 10.549033], [1.0, -0.683565, -2.166125], [1.0, 0.229456, 5.921938], [1.0, -0.959885, 11.555336], [1.0, 0.492911, 10.993324], [1.0, 0.184992, 8.721488], [1.0, -0.355715, 10.325976], [1.0, -0.397822, 8.058397], [1.0, 0.824839, 13.730343], [1.0, 1.507278, 5.027866], [1.0, 0.099671, 6.835839], [1.0, -0.344008, 10.717485], [1.0, 1.785928, 7.718645], [1.0, -0.918801, 11.560217], [1.0, -0.364009, 4.7473], [1.0, -0.841722, 4.119083], [1.0, 0.490426, 1.960539], [1.0, -0.007194, 9.075792], [1.0, 0.356107, 12.447863], [1.0, 0.342578, 12.281162], [1.0, -0.810823, -1.466018], [1.0, 2.530777, 6.476801], [1.0, 1.296683, 11.607559], [1.0, 0.475487, 12.040035], [1.0, -0.783277, 11.009725], [1.0, 0.074798, 11.02365], [1.0, -1.337472, 0.468339], [1.0, -0.102781, 13.763651], [1.0, -0.147324, 2.874846], [1.0, 0.518389, 9.887035], [1.0, 1.015399, 7.571882], [1.0, -1.658086, -0.027255], [1.0, 1.319944, 2.171228], [1.0, 2.056216, 5.019981], [1.0, -0.851633, 4.375691], [1.0, -1.510047, 6.061992], [1.0, -1.076637, -3.181888], [1.0, 1.821096, 10.28399], [1.0, 3.01015, 8.401766], [1.0, -1.099458, 1.688274], [1.0, -0.834872, -1.733869], [1.0, -0.846637, 3.849075], [1.0, 1.400102, 12.628781], [1.0, 1.752842, 5.468166], [1.0, 0.078557, 0.059736], [1.0, 0.089392, -0.7153], [1.0, 1.825662, 12.693808], [1.0, 0.197445, 9.744638], [1.0, 0.126117, 0.922311], [1.0, -0.679797, 1.22053], [1.0, 0.677983, 2.556666], [1.0, 0.761349, 10.693862], [1.0, -2.168791, 0.143632], [1.0, 1.38861, 9.341997], [1.0, 0.317029, 14.739025]]

labelMat: [0, 1, 0, 0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 0, 0, 0, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 0, 0, 1, 1, 1, 0, 1, 0, 0]


dataMat转成矩阵:

[[ 1.0000000e+00 -1.7612000e-02  1.4053064e+01]
 [ 1.0000000e+00 -1.3956340e+00  4.6625410e+00]
 [ 1.0000000e+00 -7.5215700e-01  6.5386200e+00]
 [ 1.0000000e+00 -1.3223710e+00  7.1528530e+00]
 [ 1.0000000e+00  4.2336300e-01  1.1054677e+01]
 [ 1.0000000e+00  4.0670400e-01  7.0673350e+00]
 [ 1.0000000e+00  6.6739400e-01  1.2741452e+01]
 [ 1.0000000e+00 -2.4601500e+00  6.8668050e+00]
 [ 1.0000000e+00  5.6941100e-01  9.5487550e+00]
 [ 1.0000000e+00 -2.6632000e-02  1.0427743e+01]
 [ 1.0000000e+00  8.5043300e-01  6.9203340e+00]
 [ 1.0000000e+00  1.3471830e+00  1.3175500e+01]
 [ 1.0000000e+00  1.1768130e+00  3.1670200e+00]
 [ 1.0000000e+00 -1.7818710e+00  9.0979530e+00]
 [ 1.0000000e+00 -5.6660600e-01  5.7490030e+00]
 [ 1.0000000e+00  9.3163500e-01  1.5895050e+00]
 [ 1.0000000e+00 -2.4205000e-02  6.1518230e+00]
 [ 1.0000000e+00 -3.6453000e-02  2.6909880e+00]
 [ 1.0000000e+00 -1.9694900e-01  4.4416500e-01]
 [ 1.0000000e+00  1.0144590e+00  5.7543990e+00]
 [ 1.0000000e+00  1.9852980e+00  3.2306190e+00]
 [ 1.0000000e+00 -1.6934530e+00 -5.5754000e-01]
 [ 1.0000000e+00 -5.7652500e-01  1.1778922e+01]
 [ 1.0000000e+00 -3.4681100e-01 -1.6787300e+00]
 [ 1.0000000e+00 -2.1244840e+00  2.6724710e+00]
 [ 1.0000000e+00  1.2179160e+00  9.5970150e+00]
 [ 1.0000000e+00 -7.3392800e-01  9.0986870e+00]
 [ 1.0000000e+00 -3.6420010e+00 -1.6180870e+00]
 [ 1.0000000e+00  3.1598500e-01  3.5239530e+00]
 [ 1.0000000e+00  1.4166140e+00  9.6192320e+00]
 [ 1.0000000e+00 -3.8632300e-01  3.9892860e+00]
 [ 1.0000000e+00  5.5692100e-01  8.2949840e+00]
 [ 1.0000000e+00  1.2248630e+00  1.1587360e+01]
 [ 1.0000000e+00 -1.3478030e+00 -2.4060510e+00]
 [ 1.0000000e+00  1.1966040e+00  4.9518510e+00]
 [ 1.0000000e+00  2.7522100e-01  9.5436470e+00]
 [ 1.0000000e+00  4.7057500e-01  9.3324880e+00]
 [ 1.0000000e+00 -1.8895670e+00  9.5426620e+00]
 [ 1.0000000e+00 -1.5278930e+00  1.2150579e+01]
 [ 1.0000000e+00 -1.1852470e+00  1.1309318e+01]
 [ 1.0000000e+00 -4.4567800e-01  3.2973030e+00]
 [ 1.0000000e+00  1.0422220e+00  6.1051550e+00]
 [ 1.0000000e+00 -6.1878700e-01  1.0320986e+01]
 [ 1.0000000e+00  1.1520830e+00  5.4846700e-01]
 [ 1.0000000e+00  8.2853400e-01  2.6760450e+00]
 [ 1.0000000e+00 -1.2377280e+00  1.0549033e+01]
 [ 1.0000000e+00 -6.8356500e-01 -2.1661250e+00]
 [ 1.0000000e+00  2.2945600e-01  5.9219380e+00]
 [ 1.0000000e+00 -9.5988500e-01  1.1555336e+01]
 [ 1.0000000e+00  4.9291100e-01  1.0993324e+01]
 [ 1.0000000e+00  1.8499200e-01  8.7214880e+00]
 [ 1.0000000e+00 -3.5571500e-01  1.0325976e+01]
 [ 1.0000000e+00 -3.9782200e-01  8.0583970e+00]
 [ 1.0000000e+00  8.2483900e-01  1.3730343e+01]
 [ 1.0000000e+00  1.5072780e+00  5.0278660e+00]
 [ 1.0000000e+00  9.9671000e-02  6.8358390e+00]
 [ 1.0000000e+00 -3.4400800e-01  1.0717485e+01]
 [ 1.0000000e+00  1.7859280e+00  7.7186450e+00]
 [ 1.0000000e+00 -9.1880100e-01  1.1560217e+01]
 [ 1.0000000e+00 -3.6400900e-01  4.7473000e+00]
 [ 1.0000000e+00 -8.4172200e-01  4.1190830e+00]
 [ 1.0000000e+00  4.9042600e-01  1.9605390e+00]
 [ 1.0000000e+00 -7.1940000e-03  9.0757920e+00]
 [ 1.0000000e+00  3.5610700e-01  1.2447863e+01]
 [ 1.0000000e+00  3.4257800e-01  1.2281162e+01]
 [ 1.0000000e+00 -8.1082300e-01 -1.4660180e+00]
 [ 1.0000000e+00  2.5307770e+00  6.4768010e+00]
 [ 1.0000000e+00  1.2966830e+00  1.1607559e+01]
 [ 1.0000000e+00  4.7548700e-01  1.2040035e+01]
 [ 1.0000000e+00 -7.8327700e-01  1.1009725e+01]
 [ 1.0000000e+00  7.4798000e-02  1.1023650e+01]
 [ 1.0000000e+00 -1.3374720e+00  4.6833900e-01]
 [ 1.0000000e+00 -1.0278100e-01  1.3763651e+01]
 [ 1.0000000e+00 -1.4732400e-01  2.8748460e+00]
 [ 1.0000000e+00  5.1838900e-01  9.8870350e+00]
 [ 1.0000000e+00  1.0153990e+00  7.5718820e+00]
 [ 1.0000000e+00 -1.6580860e+00 -2.7255000e-02]
 [ 1.0000000e+00  1.3199440e+00  2.1712280e+00]
 [ 1.0000000e+00  2.0562160e+00  5.0199810e+00]
 [ 1.0000000e+00 -8.5163300e-01  4.3756910e+00]
 [ 1.0000000e+00 -1.5100470e+00  6.0619920e+00]
 [ 1.0000000e+00 -1.0766370e+00 -3.1818880e+00]
 [ 1.0000000e+00  1.8210960e+00  1.0283990e+01]
 [ 1.0000000e+00  3.0101500e+00  8.4017660e+00]
 [ 1.0000000e+00 -1.0994580e+00  1.6882740e+00]
 [ 1.0000000e+00 -8.3487200e-01 -1.7338690e+00]
 [ 1.0000000e+00 -8.4663700e-01  3.8490750e+00]
 [ 1.0000000e+00  1.4001020e+00  1.2628781e+01]
 [ 1.0000000e+00  1.7528420e+00  5.4681660e+00]
 [ 1.0000000e+00  7.8557000e-02  5.9736000e-02]
 [ 1.0000000e+00  8.9392000e-02 -7.1530000e-01]
 [ 1.0000000e+00  1.8256620e+00  1.2693808e+01]
 [ 1.0000000e+00  1.9744500e-01  9.7446380e+00]
 [ 1.0000000e+00  1.2611700e-01  9.2231100e-01]
 [ 1.0000000e+00 -6.7979700e-01  1.2205300e+00]
 [ 1.0000000e+00  6.7798300e-01  2.5566660e+00]
 [ 1.0000000e+00  7.6134900e-01  1.0693862e+01]
 [ 1.0000000e+00 -2.1687910e+00  1.4363200e-01]
 [ 1.0000000e+00  1.3886100e+00  9.3419970e+00]
 [ 1.0000000e+00  3.1702900e-01  1.4739025e+01]]

对应labelMat最终转换为矩阵
[[0]
 [1]
 [0]
 [0]
 [0]
 [1]
 [0]
 [1]
 [0]
 [0]
 [1]
 [0]
 [1]
 [0]
 [1]
 [1]
 [1]
 [1]
 [1]
 [1]
 [1]
 [1]
 [0]
 [1]
 [1]
 [0]
 [0]
 [1]
 [1]
 [0]
 [1]
 [1]
 [0]
 [1]
 [1]
 [0]
 [0]
 [0]
 [0]
 [0]
 [1]
 [1]
 [0]
 [1]
 [1]
 [0]
 [1]
 [1]
 [0]
 [0]
 [0]
 [0]
 [0]
 [0]
 [1]
 [1]
 [0]
 [1]
 [0]
 [1]
 [1]
 [1]
 [0]
 [0]
 [0]
 [1]
 [1]
 [0]
 [0]
 [0]
 [0]
 [1]
 [0]
 [1]
 [0]
 [0]
 [1]
 [1]
 [1]
 [1]
 [0]
 [1]
 [0]
 [1]
 [1]
 [1]
 [1]
 [0]
 [1]
 [1]
 [1]
 [0]
 [0]
 [1]
 [1]
 [1]
 [0]
 [1]
 [0]
 [0]]
 矩阵行列
 m,n=100,3

 alpha=0.001  //每次步长

 maxCycles=500 //最大循环数

 weights：参数列表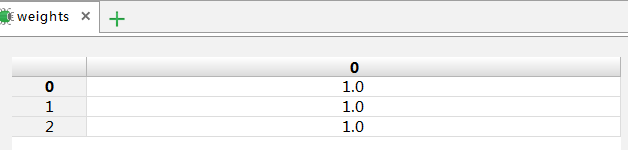




 开始执行循环处理 0-maxCycles

 利用当前dataMat和 weights 根据公式计算h=sigmoid得到结果矩阵

 h=
 [[0.9999997 ]
 [0.98616889]
 [0.99887232]
 [0.99892083]
 [0.99999619]
 [0.99979122]
 [0.99999945]
 [0.99553342]
 [0.99998516]
 [0.99998882]
 [0.99984482]
 [0.99999982]
 [0.99524519]
 [0.99975551]
 [0.99793879]
 [0.97128332]
 [0.99919801]
 [0.97477903]
 [0.77681757]
 [0.99957748]
 [0.9980066 ]
 [0.22252829]
 [0.99999498]
 [0.26394949]
 [0.8246228 ]
 [0.99999261]
 [0.99991432]
 [0.01392443]
 [0.99215449]
 [0.99999407]
 [0.99007735]
 [0.99994736]
 [0.999999  ]
 [0.05986936]
 [0.99921454]
 [0.99997998]
 [0.99997966]
 [0.99982544]
 [0.99999104]
 [0.99998525]
 [0.97919678]
 [0.99971059]
 [0.99997751]
 [0.93705909]
 [0.9890627 ]
 [0.99996675]
 [0.1359093 ]
 [0.99921684]
 [0.99999079]
 [0.99999622]
 [0.99995015]
 [0.99998279]
 [0.99982675]
 [0.99999982]
 [0.9994663 ]
 [0.99964232]
 [0.9999885 ]
 [0.99997259]
 [0.99999121]
 [0.99542831]
 [0.98631076]
 [0.96925991]
 [0.99995761]
 [0.99999899]
 [0.99999879]
 [0.21808844]
 [0.99995494]
 [0.99999908]
 [0.99999865]
 [0.99998668]
 [0.99999443]
 [0.53267014]
 [0.99999957]
 [0.97651256]
 [0.99998887]
 [0.99993141]
 [0.33507029]
 [0.98891672]
 [0.99968925]
 [0.98927143]
 [0.99613509]
 [0.03702176]
 [0.99999797]
 [0.99999593]
 [0.83044946]
 [0.17239595]
 [0.9820568 ]
 [0.9999997 ]
 [0.99973113]
 [0.75736609]
 [0.59244738]
 [0.99999982]
 [0.9999823 ]
 [0.88578868]
 [0.82357126]
 [0.98572192]
 [0.9999961 ]
 [0.26402371]
 [0.99999196]
 [0.99999989]]


 利用labelMat和h差值计算错误矩阵
 error=
 [[-9.99999705e-01]
 [ 1.38311131e-02]
 [-9.98872318e-01]
 [-9.98920829e-01]
 [-9.99996191e-01]
 [ 2.08776178e-04]
 [-9.99999448e-01]
 [ 4.46658302e-03]
 [-9.99985160e-01]
 [-9.99988817e-01]
 [ 1.55180408e-04]
 [-9.99999819e-01]
 [ 4.75480712e-03]
 [-9.99755508e-01]
 [ 2.06121361e-03]
 [ 2.87166819e-02]
 [ 8.01985278e-04]
 [ 2.52209704e-02]
 [ 2.23182435e-01]
 [ 4.22517114e-04]
 [ 1.99340232e-03]
 [ 7.77471707e-01]
 [-9.99994982e-01]
 [ 7.36050513e-01]
 [ 1.75377198e-01]
 [-9.99992607e-01]
 [-9.99914316e-01]
 [ 9.86075568e-01]
 [ 7.84550562e-03]
 [-9.99994072e-01]
 [ 9.92265048e-03]
 [ 5.26440337e-05]
 [-9.99998997e-01]
 [ 9.40130641e-01]
 [ 7.85460201e-04]
 [-9.99979982e-01]
 [-9.99979663e-01]
 [-9.99825445e-01]
 [-9.99991040e-01]
 [-9.99985247e-01]
 [ 2.08032168e-02]
 [ 2.89409924e-04]
 [-9.99977505e-01]
 [ 6.29409096e-02]
 [ 1.09372974e-02]
 [-9.99966746e-01]
 [ 8.64090701e-01]
 [ 7.83156928e-04]
 [-9.99990792e-01]
 [-9.99996222e-01]
 [-9.99950152e-01]
 [-9.99982794e-01]
 [-9.99826745e-01]
 [-9.99999824e-01]
 [ 5.33699377e-04]
 [ 3.57681460e-04]
 [-9.99988504e-01]
 [ 2.74100613e-05]
 [-9.99991206e-01]
 [ 4.57168621e-03]
 [ 1.36892448e-02]
 [ 3.07400940e-02]
 [-9.99957612e-01]
 [-9.99998988e-01]
 [-9.99998789e-01]
 [ 7.81911565e-01]
 [ 4.50551593e-05]
 [-9.99999085e-01]
 [-9.99998650e-01]
 [-9.99986683e-01]
 [-9.99994432e-01]
 [ 4.67329863e-01]
 [-9.99999571e-01]
 [ 2.34874355e-02]
 [-9.99988865e-01]
 [-9.99931409e-01]
 [ 6.64929709e-01]
 [ 1.10832850e-02]
 [ 3.10754358e-04]
 [ 1.07285749e-02]
 [-9.96135092e-01]
 [ 9.62978241e-01]
 [-9.99997965e-01]
 [ 4.06978628e-06]
 [ 1.69550543e-01]
 [ 8.27604054e-01]
 [ 1.79431989e-02]
 [-9.99999703e-01]
 [ 2.68871522e-04]
 [ 2.42633906e-01]
 [ 4.07552621e-01]
 [-9.99999818e-01]
 [-9.99982303e-01]
 [ 1.14211320e-01]
 [ 1.76428743e-01]
 [ 1.42780771e-02]
 [-9.99996103e-01]
 [ 7.35976291e-01]
 [-9.99991956e-01]
 [-9.99999894e-01]]


因为需要求得最大值时候的weights值,使用梯度上升算法的迭代公式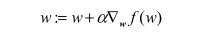

关于weights的迭代推导公式的来历详见

 根据公式利用步长alpha:1*1、error:100*1、dataMatrix.transpose():3*100和原weights:3*1计算得到下一次循环的新weights
dataMatrix(100*3)
weights(3*1)
error(100*1)

 所以
 新weights=weights+alpha*dataMatrix.transpose()*error
 =

 [[0.96358575]
 [0.98285296]
 [0.48828325]]
书中理论部分并没有讲清楚，具体解释参考下面的链接：