朴素贝叶斯分类器训练过程分析

这是一个识别论坛不当言论的案例

步骤一:获得这个问题的全部特征(标称型)
所谓标称型数据:是可以化成0 1表示的数据

用于案例训练的数据如下:
dataSet: [['my', 'dog', 'has', 'flea', 'problems', 'help', 'please'], ['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid'], ['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him'], ['stop', 'posting', 'stupid', 'worthless', 'garbage'], ['mr', 'licks', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him'], ['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']]

获得这个问题的全部特征做法如下
依次循环取得一行
document: ['my', 'dog', 'has', 'flea', 'problems', 'help', 'please']

set化可获取词列表{'please', 'has', 'flea', 'help', 'my', 'problems', 'dog'}

循环每步和上一步获得set取并集
{'please', 'maybe', 'not', 'him', 'to', 'has', 'stupid', 'flea', 'help', 'my', 'problems', 'take', 'park', 'dog'}
...

list化最终得到训练数据的不重复词库如下：
word:['love', 'please', 'not', 'has', 'how', 'stop', 'is', 'cute', 'dog', 'ate', 'worthless', 'I', 'stupid', 'flea', 'dalmation', 'problems', 'take', 'park', 'buying', 'to', 'steak', 'food', 'posting', 'quit', 'so', 'maybe', 'licks', 'him', 'mr', 'my', 'help', 'garbage']


步骤二:实现输入词条得到上一步的词库状态特征表示列表

上一步得到的不重复词库:
vocabList: ['has', 'stop', 'him', 'not', 'take', 'how', 'to', 'dalmation', 'maybe', 'is', 'food', 'steak', 'dog', 'my', 'I', 'stupid', 'posting', 'licks', 'park', 'please', 'worthless', 'problems', 'cute', 'garbage', 'ate', 'flea', 'mr', 'help', 'love', 'quit', 'buying', 'so']

举例要获取词库特征表示列表的输入语句列表表示如下
inputSet: ['dog','stop']

我们初始化一个和词库等长的表示列表
returnVec: [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]

依次判断inputSet中的单词是否在vocabList中,如果在则获得其在vocabList中的序号位置index并置returnVec
对应位置的置为1

如果发现某些单词不存在于词库中,则忽略即可

按照上面步骤通过上面的inputSet得到的表示列表为
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]

下面结合理论进行下步处理

贝叶斯准则公式: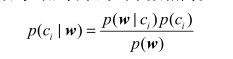


其中w是一组特征值
根据本应用场景解释,公式左边表示在语句单词出现列表为w情况下被划分到类别c的概率。
右边上面和左边刚好相反的部分公式解释是：被划分到类别c的情况下语句单词出现列表为w的概率
p(ci)为训练数据中被划分到类别ci的概率
p(w)为训练数据中出现列表为w的概率

可以简单理解贝叶斯准则做了这样一件事:巧妙的提出了一种在已知P(A|B)可求的情况下求出P(B|A)的方法

这里有一个理论上不成立但实际使用效果很好的假设:各个单词出现在不同分类的事件相互独立，其实一般是有关系的，但是应用这个假设能简化计算过程，接下来的计算会用到这个假设

根据这个假设我们可以得到p(w|c)=p(w1|c)p(w2|c)....
其中w={w1,w2...}


步骤三:朴素贝叶斯分类训练过程

1.将训练数据转化为特征值列表表示
  

2.输入条件
  (1.)trainMatrix
  (2.)trainCategory: [0, 1, 0, 1, 0, 1] 是否是不当言论

3.开始训练（训练目的,今后给出新的文档判断是否不当言论）

  上面的数据我们可以计算得到以下数据
  文档数目:6
  numWords:32 每个文档特征数
  利用trainCategory 计算可得 P(是不当言论概率) pAbusive=0.5  对应上面贝叶斯准则的p(c=1)

  初始化两个如下的numWords个值为0的数组用于状态暂存
  p0Num,p1Num
  

  p0Denom,p1Denom = 0.0
  
  遍历训练文档

  算法过程举例:
  
  如文档0类别为0
  p0Num加上trainMatrix[0]变为
  
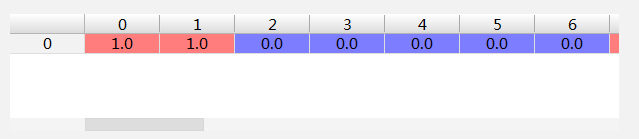
  p0Denom加上trainMatrix[0]词汇数变为7.0
  ...

  如文档1类别为1
  p1Num加上trainMatrix[1]
  p1Denom加上trainMatrix[1]词汇数变为8.0

  循环最终得到
  p0Num记录类别为0时各个特征的次数数组
  p0Denom记录类别为0时所有为0文档单词总数:24.0
  
  p1Num记录类别为1时各个特征的次数数组
  p1Denom记录类别为1时所有为1文档单词总数:19.0

  通过公式
  p1Vec = p1Num / p1Denom
  对应上面的贝叶斯准则可以得到p(w1|c=1) p(w2|c=1).....
  
  同样通过公式
  p0Vec = p0Num / p0Denom
  对应上面的贝叶斯准则可以得到p(w1|c=0) p(w2|c=0).....

  至此我们需要的几个关键概率都已经计算出来了


改进:
1. p(w 0 |1)p(w 1 |1)p(w 2 |1) 。如果其中一个概率值为0，那么最后的乘积也为0。为降低这种影响，可以将所有词的出现数初始化为1，并将分母初始化为2

2.当计算乘积p(w 0 |c i )p(w 1 |c i )p(w 2 |c i )...p(w N |c i ) 时，由于大部分因子都非常小，所以程序会下溢出或者得到不正确的答案通过求对数可以避免下溢出或者浮点数舍入导致的错误

利用分类器进行真实分类
输入:listOPosts,listClasses 第一个存储文档，第二个存储文档标记类别
testEntry=['love','my','dalmation'] 要测试分类的句子词组

根据listOPosts,listClasses计算得到
p0V,用于计算p(w|(c=0))
p1V,用于计算p(w|(c=1))
pAb,p(c=1)概率

利用listOPosts 生成testEntry的词向量数组表示
thisDoc=[...]

利用thisDoc,p0V,p1V,pAb计算testEntry属于的类别

因为我们只需要比较p(c=1|w)和p(c=0|w)的大小 而p(w)是固定的,所以上面的公式取对数之后只需要计算
p1=sum(thisDoc*p1V)+np.log(pAb)
p0=sum(thisDoc*p0V)+np.log(1.0-pAb)

因为其中thisDoc记录了单词是否出现，所以对应单个单词出现就是p0V或者p1V概率，不出现自然就是0

比较上面的p0、p1大小即可知道最终分类
这个例子
p0=-7.694848072384611
p1=-9.826714493730215
因为p0>p1所以被归类为0

 
算法持续改进:
问题:如果一个词在文档中出现不止一次，这可能意味着包含该词是否出现在文档中所不能表达的某种信息，这种方法被称为词袋模型
改进:
修改每次遇到单词对应记录不是置为1而是+1